The Walking Dead Model

Today, I finally discovered a useful application of my chemical engineering degree. To initiate engaging philosophical and mathematical conversations about zombies with grumpy old men.

As I sat at my terminal watching the first episode of The Walking Dead, a raspy voice next to me muttered, "That would never happen."

I replied with the usual, "Yes, I know zombies don't exist." Usually that avoids the unwanted confrontation and allows for a change of subject. It is a formulaic reply that Dale Carnegie would use - if he was a zombie enthusiast. Then he took me by surprise when he explained that the population of a small town would not be completely zombified or dead.

In all honesty, I have wondered what I would do in certain zombie apocalypse scenarios. But I have never thought about the larger picture like the population of a town. With a few Auntie Anne's napkins and 45 minutes before boarding we began outlining a population model using the zombie rules from the universe of The Walking Dead.

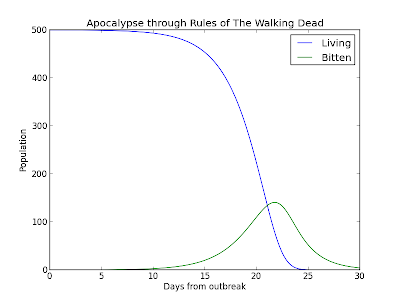
In The Walking Dead, every person possesses some type of dormant infection that will turn people who die of natural causes into zombies. The bites from these zombies will turn the living into zombies after a period of time. Zombies can be annihilated by the destruction of the reptilian brain. For those readers who are chemical engineers, you should notice that these rules are mathematically very similar to a time dependent batch reaction. The correct model is a simple mass balance, since bodies are conserved.

The balance for those who are living includes births, non-zombie related deaths, and those who are bitten from zombie related encounters, respectively:

\[\frac{dL}{dt}=B-nL-xLZ\]

The balance for those who are actively infected includes those who are bitten from zombie related encounters, those who turn into zombies, and the ones that die from non-zombie related causes, respectively:

\[\frac{dI}{dt}=xLZ-pI-nI\]

The balance for zombies contains those who turn into zombies from bites, those who are resurrected from non-zombie related deaths, and those who are killed by an encounter with the living, respectively:

\[\frac{dZ}{dt}=pI-rT-aLZ\]

The final balance is a "kill" count that includes the living who died of non-zombie related causes, the actively infected who die of 'natural' causes, zombies that have been destroyed, and the dead who have been resurrected into zombies, respectively:

\[\frac{dT}{dt}=nL+nI+aLZ-rT\]

Here is a summary of the notation I used in my model:

• L: the number of living
• I: the number of bitten
• Z: the number of zombies
• T: the number of people "killed"
• B: the population birth rate
• n: the chance of a non-zombie related death
• x: the chance of living being bitten in a zombie encounter
• p: the chance of a bitten person turning into a zombie
• r: the chance a dead person is resurrected into a zombie
• a: the chance a zombie is totally destroyed

Without access to Mathematica on my laptop, I had to resort to a more old school method, Python. The development of the model and coding went pretty smoothly. It was coming to an agreement on the probabilities of the model that caused us to leave our discussion unresolved before zone 4 boarding. To Tim the taxidermist from Texas and my blog readers, please tell me what you think plausible probabilities are, using the model in the following python code.
# modeling the walking dead import numpy as np import matplotlib.pyplot as plt from scipy.integrate import odeint B = 0 # births n = 0.0001 # natural death probability (per day) x = 0.0055 # transmission probability (per day) r = 0.9000 # resurrect probability (per day) a = 0.0075 # destroy probability (per day) p = 0.5000 # infection probability (per day) # solve the system dy/dt = f(y, t) def f(y, t): Li = y[0] Ii = y[1] Zi = y[2] Ti = y[3] # our modeling equations f0 = B - x*Li*Zi - n*Li f1 = x*Li*Zi - p*Ii - n*Ii f2 = p*Ii + r*Ti - a*Li*Zi f3 = n*Li + n*Ii + a*Li*Zi - r*Ti return [f0, f1, f2, f3] # initial conditions L0 = 500 # initial population I0 = 0 # initial infected population Z0 = 0 # initial zombie population T0 = 0 # initial death population y0 = [L0, I0, Z0, T0] # initial condition vector t = np.linspace(0, 30, 5000) # time grid # solve the DEs soln = odeint(f, y0, t) L = soln[:, 0] I = soln[:, 1] Z = soln[:, 2] T = soln[:, 3] # plot results plt.figure() plt.plot(t, L, label='Living') plt.plot(t, Z, label='Zombies') plt.xlabel('Days from outbreak') plt.ylabel('Population') plt.title('Apocalypse through Rules of The Walking Dead') plt.legend(loc=0) #plt.show() plt.figure() plt.plot(t, L, label='Living') plt.plot(t, I, label='Bitten') plt.xlabel('Days from outbreak') plt.ylabel('Population') plt.title('Apocalypse through Rules of The Walking Dead') plt.legend(loc=0) plt.show() The probabilities used in my code were found through some trial and error to closely match those in The Walking Dead series on AMC. Assuming that the zombie outbreak began when Rick Grimes was shot, Rick was in a coma for about three weeks before the military is seen opening fire on the hoards of zombies at the hospital. Then a few days later Rick wakes up to find no living person around. The plots created from the model above replicates this timing pretty well.