A hidden Markov model is not that hard of a conceptual stretch when applied to crime modeling. Lets assume that all criminal activities in Chicago evolved according to a Markov process, which may have a finite or infinite amount of states. The underlying Markov process is not directly observable because these states are hidden. Luckily, for each state there is an associated stochastic process which produces an observable signal (a crime report). So as this criminal system in Chicago evolves over time, delegated by the hidden Markov chain, it produces crime reports as observable outcomes.
For a full explanation of the mathematical theory behind HMMs please refer to this article by Lawrence Rabiner. Even though Rabiner focuses on HMM applications to speech recognition, it covers in great detail the theory used in my implementation. To simplify things for myself and to cut down on computation time, I created a hidden Markov model with univariate Gaussian outcomes. The model is fitted using a maximum likelihood estimation, where the values of the parameters are those that maximizes the likelihood of the observed data. Here, I used the Baum-Welch Algorithm for estimating the maximum likelihood.
The observed Chicago crime data is the total number of daily reported crimes between July 1, 2011 and March 31, 2012. A log difference transformation of this data was performed to create a more normal distribution of observables. This is all done in Mathematica with six lines of code:
csv = Import[
"https://data.cityofchicago.org/api/views/x2n5-8w5q/rows.csv",
"CSV"];
start = "07/01/2011"; end = "03/31/2012";
range = Join[
First[Position[
If[StringMatchQ[#, start ~~ __], 1, 0] & /@
Drop[csv, 1][[All, 2]], 1]] + 1,
Last[Position[
If[StringMatchQ[#, end ~~ __], 1, 0] & /@
Drop[csv, 1][[All, 2]], 1]] + 1];
crimeseries =
Tally[DateString[
DateList[{ToString[#], {"Month", "/", "Day", "/", "Year", " ",
"Hour12", ":", "Minute", " ", "AMPM"}}], {"MonthName", " ",
"Day", " ", "Year"}] & /@ Take[csv, range][[All, 2]]];
The HMM fitting of the crime data uses three functions I created in Mathematica:
MarkovChainEquilibrium[TransitionMatrix_] :=
Inverse[Transpose[TransitionMatrix] -
IdentityMatrix[Length[TransitionMatrix]] + 1].ConstantArray[1,
Length[TransitionMatrix]];
RandomInitial[Data_, States_] := Module[
{TransMat, i, vnGamma, ProbVec, StateMean, vnQ, StateStD, t, mnW},
TransMat = (#/Total[#]) & /@ (RandomReal[{0.01, 0.99}, {States,
States}]);
ProbVec = MarkovChainEquilibrium[TransMat];
StateMean = ((#/Total[#]) &[
RandomReal[{-0.99, 0.99}, States]]) Mean[Data];
StateStD =
Sqrt[((#/Total[#]) &[RandomReal[{0.1, 0.99}, States]]) Variance[
Data]];
{ProbVec, TransMat, StateMean, StateStD}];
Options[HMM] = {"LikelihoodTolerance" -> 10^(-7),
"MaxIterations" -> 500};
HMM[Data_, {InitialIota_, InitialA_, InitialMean_, InitialStD_},
OptionsPattern[]] := Module[
{TransMat, matAlpha, matB, matBeta, nBIC, matGamma, ProbVec,
StateLogLikelihood, iMaxIter, StateMean, iN, StateNu, StateStD, t,
iT, nTol, matWeights, matXi},
nTol = OptionValue["LikelihoodTolerance"];
iMaxIter = OptionValue["MaxIterations"];
iT = Length[Data]; iN = Length[InitialA];
ProbVec = InitialIota; TransMat = InitialA;
StateMean = InitialMean; StateStD = InitialStD;
matB =
Table[PDF[NormalDistribution[StateMean[[#]], StateStD[[#]]],
Data[[t]]] & /@ Range[iN], {t, 1, iT}];
matAlpha = Array[0. &, {iT, iN}];
StateNu = Array[0. &, iT];
matAlpha[[1]] = ProbVec matB[[1]];
StateNu[[1]] = 1/Total[matAlpha[[1]]];
matAlpha[[1]] *= StateNu[[1]];
For[t = 2, t <= iT, t++,
matAlpha[[t]] = (matAlpha[[t - 1]].TransMat) matB[[t]];
StateNu[[t]] = 1/Total[matAlpha[[t]]];
matAlpha[[t]] *= StateNu[[t]]];
StateLogLikelihood = {-Total[Log[StateNu]]};
Do[matBeta = Array[0. &, {iT, iN}];
matBeta[[iT, ;;]] = StateNu[[iT]];
For[t = iT - 1, t >= 1, t--,
matBeta[[t]] =
TransMat.(matBeta[[t + 1]] matB[[t + 1]]) StateNu[[t]]];
matGamma = (#/Total[#]) & /@ (matAlpha matBeta);
matXi = Array[0. &, {iN, iN}];
For[t = 1, t <= iT - 1, t++,
matXi += (#/Total[Flatten[#]]) &[
TransMat KroneckerProduct[matAlpha[[t]],
matBeta[[t + 1]] matB[[t + 1]]]]];
TransMat = (#/Total[#]) & /@ matXi;
ProbVec = matGamma[[1]];
matWeights = (#/Total[#]) & /@ Transpose[matGamma];
StateMean = matWeights.Data;
StateStD = Sqrt[Total /@ (matWeights (Data - # & /@ StateMean)^2)];
matB =
Table[PDF[NormalDistribution[StateMean[[#]], StateStD[[#]]],
Data[[t]]] & /@ Range[iN], {t, 1, iT}];
matAlpha = Array[0. &, {iT, iN}];
StateNu = Array[0. &, iT];
matAlpha[[1]] = ProbVec matB[[1]];
StateNu[[1]] = 1/Total[matAlpha[[1]]];
matAlpha[[1]] *= StateNu[[1]];
For[t = 2, t <= iT, t++,
matAlpha[[t]] = (matAlpha[[t - 1]].TransMat) matB[[t]];
StateNu[[t]] = 1/Total[matAlpha[[t]]];
matAlpha[[t]] *= StateNu[[t]]];
StateLogLikelihood =
Append[StateLogLikelihood, -Total[Log[StateNu]]];
If[StateLogLikelihood[[-1]]/StateLogLikelihood[[-2]] - 1 <= nTol,
Break[]],
{iMaxIter}];
nBIC = -2 StateLogLikelihood[[-1]] + (iN (iN + 2) - 1) Log[iT];
{"\[Iota]" -> ProbVec, "a" -> TransMat, "\[Mu]" -> StateMean,
"\[Sigma]" -> StateStD, "\[Gamma]" -> matGamma, "BIC" -> nBIC,
"LL" -> StateLogLikelihood}];
The first function computes the equilibrium distribution for an ergodic Markov chain. The second function generates a random parameter set with inputs of the observed data and the number of states. Output from the second function is a list containing the initial state probability vector, the transition matrix of the Markov chain, the mean of each state, and the standard deviation of each state. The third function is the maximum likelihood estimated fit of the HMM. It takes inputs of the observed data and a random parameter set from the second function. The output from the third function is a list that contains the initial state probability vector, the transition matrix, the mean vector, the standard deviation vector, a vector of periodic state probabilities, the Bayesian Information Criterion (BIC) for the fit, and a history of the loglikelihood for each iteration.As an example of how to use these functions, lets generate a two state fit with the log differenced crime data. The first step is to generate a random initial parameter set. To hedge the risk of generating a few really bad initial guesses I chose to generate a set of 20 initial guess and run them for 10 iterations. From this set, I then chose the candidate with the highest loglikelihood. This candidate will then be used as a starting point for fitting the model.
guess = HMM[crimedifference[[All, 2]], #, "MaxIterations" -> 10] & /@
Table[RandomInitial[crimedifference[[All, 2]], 2], {20}];
bestguessLL =
Flatten[Position[#, Max[#]] &[Last["LL" /. #] & /@ guess]][[1]];
hmmfit = HMM[
crimedifference[[All,
2]], {"\[Iota]", "a", "\[Mu]",
"\[Sigma]"} /. (guess[[bestguessLL]])];
It is usually a good idea to check the convergence of the likelihood function to make sure nothing has gone awry.
ListPlot["LL" /. hmmfit, PlotRange -> All]
To cut down on unnecessary typing, I have written a Do loop to evaluate models with different number of states and used a For loop to create a table of the different models with their associated BIC.
MaxGaussians = 3;
Do[InitialGuess["Crimes", i] =
HMM[crimedifference[[All, 2]], #, "MaxIterations" -> 10] & /@
Table[RandomInitial[crimedifference[[All, 2]], i], {20}];
BestGuessLL["Crimes", i] =
Flatten[Position[#, Max[#]] &[
Last["LL" /. #] & /@ InitialGuess["Crimes", i]]][[1]];
FittedHMM["Crimes", i] =
HMM[crimedifference[[All,
2]], {"\[Iota]", "a", "\[Mu]",
"\[Sigma]"} /. (InitialGuess["Crimes", i][[
BestGuessLL["Crimes", i]]])],
{i, 1, MaxGaussians, 1}]
bic = {}; states = {};
For[i = 1, i < MaxGaussians + 1, i++, AppendTo[states, i];
j = "BIC" /. FittedHMM["Crimes", i]; AppendTo[bic, j]]
TableForm[Transpose[{states, bic}],
TableHeadings -> {None, {"#States", "BIC"}},
TableAlignments -> Center]
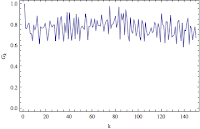
By the BIC, it seems that a HMM with two univariate Gaussian states is the best model. If we examine the Markov chain equilibrium distribution, it seems crimes in Chicago are at a highly volatile with decreasing crimes state about 91% of the time and a low volatility with moderate increases in crimes state about 9% of the time. Looking at the main diagonal of the transition matrix, the large transitions indicate that if crimes in Chicago are found in one state then it will stay in that state for a while.
Print["Equilibrium Distribution = ", MatrixForm[MarkovChainEquilibrium["a" /. FittedHMM["Crimes", 2]]]] Print["Transition Matrix from Data = ", MatrixForm["a" /. FittedHMM["Crimes", 2]]]
That is all for now, I'll try to create a simulation with the HMM data for the next post. All the files used for this post can be found here.